Содержание
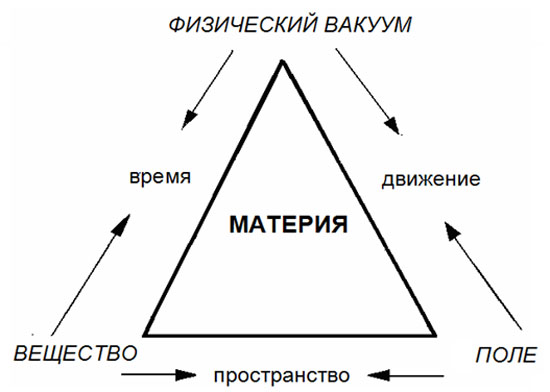
4.2.5. Физический вакуум
Вакуум
в переводе с латинского (vacuum)
означает
пустоту.
Еще
в античности был поставлен вопрос о
том, пусто мировое пространство
или заполнено некой материальной средой,
чем-то, отличающимся
от пустоты.
Согласно
философской концепции великого
древнегреческого философа
Демокрита,
все
вещества состоят из частиц, между
которыми
находится пустота. Но согласно философской
концепции другого
не менее знаменитого древнегреческого
философа Аристотеля,
в
мире нет ни малейшего места, где не было
бы «ничего». Эта среда, пронизывающая
все пространства Вселенной, была
названа эфиром.
Понятие
«эфира» вошло в европейскую науку.
Великий Ньютон понимал, что закон
всемирного тяготения будет иметь смысл,
если пространство обладает физической
реальностью, т.е. представляет собой
среду, обладающую физическими свойствами.
Он писал:
«Мысль о том… чтобы одно тело могло
воздействовать на другое
через пустоту на расстоянии, без участия
чего-то такого, что
переносило бы действие и силу от одного
тела к другому, — представляется
мне нелепой»1.
В
классической физике не было экспериментальных
данных, которые
подтверждали бы существование эфира.
Но не было и данных, которые
бы опровергали это. Авторитет Ньютона,
способствовал тому, что эфир стал
рассматриваться в качестве важнейшего
понятия физики. Под понятие «эфир» стали
подводить все, что вызывалось
гравитационными и электромагнитными
силами. Но поскольку другие
фундаментальные взаимодействия до
возникновения атомной физики
практически не изучались, то с помощью
эфира брались объяснять
любые явления и любой процесс.
Эфир
должен был обеспечивать действие закона
всемирного тяготения;
эфир оказывался средой, по которой идут
световые волны;
эфир нес ответственность за все проявления
электромагнитных
сил. Развитие физики заставляло наделять
эфир все новыми
и новыми противоречивыми свойствами.
Опыт
Майкельсона, величайший из всех
«отрицательных» опытов
в истории науки, привел к выводу, что
гипотеза неподвижного мирового
эфира, на которую классическая физика
возлагала боль-
1
Цит.
по: Ливанова
А Три
судьбы постижения мира. Жизнь замечательных
идей. — М:
Знание, 1969. — С. 122.
122
шие
надежды, неверна. Рассмотрев все
предположения относительно
эфира со времен Ньютона и до начала XX
в., А. Эйнштейн в труде
«Эволюция физики» подвел итоги: «Все
наши попытки сделать эфир реальным
провалились. Он не обнаружил ни своего
механического строения, ни абсолютного
движения. От всех свойств эфира
не осталось ничего… Все попытки открыть
свойства эфира привели
к трудностям и противоречиям. После
стольких неудач наступает
момент, когда следует совершенно забыть
об эфире и постараться
никогда больше не упоминать о нем»1.
В
специальной теории относительности
произошел отказ от понятия
«эфира».
В
общей теории относительности в качестве
материальной среды,
взаимодействующей с телами, обладающими
гравитационными
массами, рассматривалось пространство.
Сам творец общей
теории относительности полагал, что
некая вездесущая материальная среда
все-таки должна существовать и обладать
определенными
свойствами. После публикации работ по
После публикации работ по
общей теории относительности
Эйнштейн неоднократно возвращался к
понятию «эфира»
и считал, что «мы не можем в теоретической
физике обойтись
без эфира, то есть континуума, наделенного
физическими
свойствами»2.
Однако
понятие «эфир» уже принадлежало истории
науки, возврата
к нему не было, а «континуум, наделенный
физическими свойствами»
был назван физическим вакуумом.
В
современной физике считается, что роль
фундаментальной материальной основы
мира выполняет физический вакуум,
который
представляет собой универсальную среду,
пронизывающую все
пространство. Физический вакуум — это
такая непрерывная среда,
в которой нет ни частиц вещества, ни
поля и вместе с тем он
является физическим объектом, а не
лишенным всяких свойств «ничто».
Непосредственно физический вакуум не
наблюдается, в экспериментах
наблюдается лишь проявление его свойств.
Принципиальное
значение для решения проблем вакуума
имеют
работы П.
Дирака. До
их появления считалось, что вакуум есть
чистое «ничто», которое каким бы
преобразованиям ни подвергать,
измениться не способно. Теория Дирака
открыла путь к преобразованиям
вакуума, в которых прежнее «ничто»
обращалось бы
во множество пар «частица — античастица».
1Эйнштейн
А. Собр.
научных трудов. — Т. IV.
— М.: Наука, 1967. — С. 467—468.
2 Там
же. Т. II.
— М.: Наука, 1966. — С. 160.
123
Вакуум
у Дирака представляет собой море
электронов с отрицательной
энергией как однородный фон, не влияющий
на прохождение
в нем электромагнитных процессов. Мы
не наблюдаем электронов
с отрицательной энергией именно потому,
что они образуют
сплошной невидимый фон, на котором
происходят все мировые
события. Наблюдаемыми могут быть только
изменения состояния
вакуума, его «возмущения».
Когда
в море электронов попадает богатый
энергией световой квант
— фотон, то он вызывает возмущение и
электрон с отрицательной
энергией может перескочить в состояние
с положительной
энергией, т. е. будет наблюдаться как
е. будет наблюдаться как
свободный электрон. Тогда
в море отрицательных электронов
образуется «дырка» и родится
пара: электрон + дырка.
Первоначально
предполагалось, что дырками в дираковском
вакууме являются протоны, единственные
известные в то время элементарные
частицы с противоположным электрону
зарядом. Однако
этой гипотезе не суждено было выжить:
в эксперименте
аннигиляцию
электрона с протоном
никто
никогда не
наблюдал.
Вопрос
о реальном существовании и физическом
смысле дырок
был решен в 1932 г. американским физиком
К.А.
Андерсеном, занимавшимся
фотографированием треков приходящих
из космоса частиц в магнитном поле. Он
обнаружил в космических лучах след
неизвестной ранее частицы, по всем
параметрам тождественной
электрону, но имеющей заряд противоположного
знака.
Эта частица была названа позитроном.
При сближении с электроном
позитрон аннигилирует с ним на два
фотона высокой
энергии (гамма-кванты), необходимость
возникновения которых обусловлена
законами сохранения энергии и импульса:
Впоследствии
оказалось, что почти все элементарные
частицы (даже
не имеющие электрических зарядов) имеют
своих «зеркальных»
двойников — античастицы, способные
аннигилировать
с ними. Исключение составляют лишь
Исключение составляют лишь
немногие истинно нейтральные
частицы, например фотоны, которые
тождественны
своим античастицам.
Огромная
заслуга П. Дирака заключалась в том, что
он разработал релятивистскую теорию
движения электрона, предсказавшую
позитрон, аннигиляцию и рождение из
вакуума элек-тронно-позитронных
пар. Стало ясно, что вакуум обладает
слож-
124
ной
структурой, из которой могут рождаться
пары: частица + античастица.
Эксперименты на ускорителях подтвердили
это предположение.
Одной
из особенностей вакуума является наличие
в нем полей
с энергией, равной нулю, и без реальных
частиц. Возникает вопрос: как может
существовать электромагнитное поле
без фотонов,
электронно-позитронное поле без
электронов и позитронов
и т.д.
Для
объяснения нулевых колебаний полей в
вакууме было введено
понятие виртуальной (возможной) частицы
— частицы с
очень малым сроком жизни порядка 10—21
— 10-24
с. Это и объясняет, почему в вакууме
Это и объясняет, почему в вакууме
постоянно рождаются и исчезают частицы
— кванты соответствующих полей. Отдельные
виртуальные частицы
нельзя обнаружить в принципе, но их
суммарное воздействие
на обычные микрочастицы обнаруживается
экспериментально.
Физики считают, что абсолютно все
реакции, все взаимодействия
между реальными элементарными частицами
происходят
при непременном участии вакуумного
виртуального фона, на который элементарные
частицы тоже влияют. Обычные частицы
порождают
виртуальные частицы. Электроны, например,
постоянно
испускают и тут же поглощают виртуальные
фотоны.
Дальнейшие
исследования квантовой физики были
посвящены
изучению возможности появления из
вакуума реальных частиц,
теоретическое обоснование которой было
дано Э.
Шредингером
в 1939 г.
В
настоящее время концепция физического
вакуума, наиболее полно разработанная
в трудах академика РАЕН Г.И.
Шипова1,
является
дискуссионной: имеются как сторонники,
так и противники
его теории.
В
1998 г. Г.И. Шипов разработал новые
фундаментальные уравнения,
описывающие структуру физического
вакуума. Эти уравнения представляют
собой систему нелинейных дифференциальных
уравнений первого порядка, в которую
входят геометризи-рованные уравнения
Гейзенберга, геометризированные
уравнения Эйнштейна
и геометризированные уравнения Янга —
Милса. Пространство
— время в теории Г.И. Шипова не только
искривлено, как
в теории Энштейна, но и закручено, как
в геометрии Римана — Картана.
Французский математик Эли
Картон первым
высказал мысль
о том, что в природе должны существовать
поля, порождаю-
Шипов Г.И. Теория
физического вакуума. Новая парадигма.
— М.: НТ-Центр, 1993.
125
щиеся
вращением. Эти поля получили названия
полей кручения. Для
учета кручения пространства Г.И. Шиповым
было введено в геометризированные
уравнения множество угловых координат,
что позволило
использовать в теории физического
вакуума угловую метрику, определяющую
квадрат бесконечно малого поворота
четырехмерной
системы отсчета1.
Добавление
вращательных координат, при помощи
которых описывается
поле кручения, привело к распространению
принципа относительности на физические
поля: все физические поля, входящие в
уравнения вакуума, имеют относительный
характер.
Уравнения
вакуума после соответствующих упрощений
приводят
к уравнениям и принципам квантовой
теории. Полученная таким
образом квантовая теория оказывается
детерминированной,
хотя
вероятностная трактовка поведения
квантовых объектов
остается неизбежной. Частицы представляют
собой предельный
случай чисто полевого образования при
стремлении массы (или
заряда) этого образования к постоянной
величине. В данном
предельном случае происходит возникновение
корпуску-лярно-волнового дуализма.
Поскольку не учитывается относительный
характер физических полей, связанный
с вращением, то
квантовая
теория не является полной и тем самым
подтверждаются
предположения А. Эйнштейна о том, что
«более совершенная
квантовая теория может быть найдена на
пути расширения
принципа относительности»2.
Вакуумные
уравнения Шилова описывают искривленное
и закрученное пространство — время,
истолковываемое как вакуумные
возбуждения, находящиеся в виртуальном
состоянии.
В
основном состоянии абсолютный вакуум
имеет нулевые средние
значения момента импульса и других
физических характеристик
и в невозмущенном состоянии наблюдаем.
Разные состояния вакуума возникают при
его флуктуациях.
Если
источником возмущения является заряд
q,
то
его состояние
проявляется как электромагнитное поле.
Если
источником возмущения является масса
т,
то
состояние
вакуума характеризуется как гравитационное
поле, что впервые
было высказано А.Д. Сахаровым3.
1Шипов
Г.И. Теория
физического вакуума. — М.: МНТЦ ВЕНТ,
1992. — С. 6.
2 Там
же. С. 9.
Сахаров А.Д.
Вакуумные
вантовые флуктуации в искривленном
пространстве и теория гравитации//Доклады
АН СССР. — Т. 177. —1967. — №1. — С. 70—71.
— Т. 177. —1967. — №1. — С. 70—71.
126
Если
источником возмущения является спин,
то состояние вакуума
интерпретируется как спиновое поле,
или торсионное поле (поле
кручения).
Исходя
из того что физический вакуум — это
динамическая система, обладающая
интенсивными флуктуациями, физики
полагают, что вакуум является источником
материи и энергии как уже
реализованных во Вселенной, так и
находящихся в скрытом состоянии. По
словам академика Г.И.
Наана, «вакуум
есть все, и все
есть вакуум».
4.3.
Мегамир: современные астрофизические
и
космологические концепции
Мегамир,
или космос, современная наука рассматривает
как взаимодействующую
и развивающуюся систему всех небесных
тел.
Мегамир имеет системную организацию в
форме планет и планетных
систем, возникающих вокруг звезд и
звездных систем — галактик.
Все
существующие галактики входят в систему
самого высокого порядка
— Метагалактику. Размеры Метагалактики
Размеры Метагалактики
очень велики:
радиус космологического горизонта
составляет 15—20 млрд световых
лет.
Понятия
«Вселенная» и «Метагалактика» — очень
близкие понятия:
они характеризуют один и тот же объект,
но в разных аспектах.
Понятие «Вселенная»
обозначает
весь существующий материальный
мир; понятие «Метагалактика»
—
тот же мир, но с точки
зрения его структуры — как упорядоченную
систему галактик.
Строение
и эволюция Вселенной изучаются
космологией.
Космология
как раздел естествознания находится
на своеобразном стыке
науки, религии и философии. В основе
космологических моделей Вселенной
лежат определенные мировоззренческие
предпосылки, а сами эти модели имеют
большое мировоззренческое значение.
10.17. Эфир и физический вакуум
| В. И. ЕЛИСЕЕВ ВВЕДЕНИЕ В МЕТОДЫ ТЕОРИИ
| |
|
10.17. ЭФИР И ФИЗИЧЕСКИЙ ВАКУУМ
Евклидово пространство, Риманово пространство, Пространство Минковского, Тензорное пространство могут рассматриваться как арена абсолютного пространства, в котором реализуются все явления материального вида. Эта иллюзия возникает в результате неверного математического аппарата.
Комплексное пространство в самом общем виде не может быть ареной, оторванной от материального мира, так как оно изначально содержит объекты, которые отождествляются с материальными объектами.
Рассмотрим этот момент более подробно
Первые две координаты отождествляются с пространством -квантов совместно с третьей координатной осью определяют пространство нейтрино. Вернее три координатные оси определяют пространство, в котором при определенных энергетических условий, могут локализоваться микрочастицы нейтринного уровня. Четвертая координата совместно с первыми тремя определяет пространство Лептонов. Пятая координата совместно с четырьмя первыми определяет пространство, в котором могут локализоваться барионные и мезонные микрочастицы. Координатные оси по структуре представляют вложенные друг в друга пространства без дополнительных условий
Комплексные координаты отрицают существование пустого пространства без материи как арену материи и взаимодействия. Координаты неотделимы от материи. Абсолютное пространство, которое иллюзорно возникает из декартовых координат, привело к отрицанию эфира и вакуума в теории А.Эйнштейна.
Абсолютное пространство, которое иллюзорно возникает из декартовых координат, привело к отрицанию эфира и вакуума в теории А.Эйнштейна.
Таким образом, комплексное пространство без локализованных частиц и микрочастиц и полей взаимодействия можно отождествить с эфиром.
Пространство, заполненное полями взаимодействия, можно отождествить с вакуумом. Реальное пространство нельзя освободить от полей взаимодействия, в связи с этим пространство чисто математически является эфиром. Пространство с полями взаимодействия будет соответствовать физическому вакууму.
Квантовая электродинамика, основателем которой считается П.Дирак, описывает физический вакуум как некоторое латентное состояние (скрытое) электронов и позитронов. Пространство латентное состояние всех частиц и античастиц не только электронов и позитронов. К настоящему времени считается, что физический вакуум не имеет не массы ни заряда, ни каких-либо других физических характеристик. Однако в малых пространственных областях до см вакуум имеет значение физических характеристик отличных от нуля. С этой физической трактовкой пространство согласуется, так как пространство координатных осей отождествляется с пространством вложенных микрочастиц.
Однако в малых пространственных областях до см вакуум имеет значение физических характеристик отличных от нуля. С этой физической трактовкой пространство согласуется, так как пространство координатных осей отождествляется с пространством вложенных микрочастиц.
В квантовой теории поля вводится понятие “ виртуальных частиц “, которые непрерывно рождаются и сразу же уничтожаются. Виртуальные частицы считается, участвуют во взаимодействии как реальные.
Согласно формулам аннигиляция (сравни формулы 10.16.11-10.16.16) электрона и позитрона приведет к росту массы в пространстве. Также обстоят дела и с другими частицами и античастицами. В связи с этим понятие виртуальной частицы требует уточнения. Аннигиляцию в вакууме необходимо рассматривать как взаимодействие полупространств, входящих в определение микрочастицы.
Если рассматривать процесс аннигиляции электрона и позитрона, то необходимо воспользоваться формулами, которые не приводят к изменению состояния пространства
Локализованный в пространстве электрон определяется двумя отрицательно заряженными полусферами. Аналогично обстоят дела и с позитроном. Поэтому в вакууме возникают виртуальные частицы с заряженными полусферами, которые аннигилируют, не вызывая изменений и нарушения закона сохранения энергии.
Аналогично обстоят дела и с позитроном. Поэтому в вакууме возникают виртуальные частицы с заряженными полусферами, которые аннигилируют, не вызывая изменений и нарушения закона сохранения энергии.
Аннигиляция этих двух полусфер приводит пространство в прежнее невозмущенное состояние
Пространство вернулось в невозбужденное состояние. Фронт электромагнитной волны это разложение пространства на две полусферы разных электрических зарядов. После прохождения фронта точки пространства возвращаются в невозбужденное состояние.
Таким образом Вакуум имеет определенное физическое состояние, характеризующееся возможностью возникновения в любой его точке частиц –аналогов частицам микромира, начиная от пар нейтрино-антинейтрино, электрона-позитрона, и до протона –антипротона. Однако по структуре виртуальные частицы представляют не полное разложение пространства в отдельности на частицу и ее античастицу, так как в этом случае при
аннигиляции произошел бы переход энергии возбуждения в массу Вакуума.
Поэтому, например электромагнитная волна при прохождении через Вакуум не теряет своей энергии и сложилась иллюзия, что для электромагнитной волны для ее распространения не требуется передаточная среда.
Если энергия фронта взаимодействия, проходящего через Вакуум, будет достаточной для разложения точек пространства на частицы и античастицы в полном смысле этого слова, то после прохождения фронта Вакуум останется в возбужденном состоянии, а аннигиляции возникших частиц приведет к образованию дополнительной, нейтральной массы и энергии.
Локализованные динамические образования в Вакууме, представляющие частицы характеризуются определенным набором и объемом математических операций по выделению комбинаций подпространств, отождествляемых с частицами из общего пространства. Само пространство обладает минимальным количеством таких операций при своем построении. В этом плане за каждой математической операцией, характеризующей изменение структуры пространства или входящего в него подпространства, стоит ее энергетическая характеристика.
На современном математическом языке структура геометрии задается выражением квадрата расстояния между соседними близкими точками. В декартовых координатах евклидова пространства квадрат такого расстояния имеет вид
Пространственная точка, соответствующая этому интервалу, представляет совмещение значений координат (x,y,z). Совмещение значений координат в одной точке пространства, а также выражение интервала, есть результат абстрактного представления о структуре пространства и являются допущениями, которые не соответствуют реальному физическому пространству, а абстрагируются из него как частный случай. Если квадрат расстояния равен нулю, то рассматривается одна и тажа точка.
Если рассмотреть комплекс , в котором все параметры действительные величины, то модуль этого комплекса будет равен интервалу
. Комплекс при этом имеет вид , так что . При этом, если имеем , то
. При этом, как было неоднократно показано, если модуль равен корню из нуля (при этом интервал считали бы нулем) имеем две разные точки.
При этом, как было неоднократно показано, если модуль равен корню из нуля (при этом интервал считали бы нулем) имеем две разные точки.
Таким образом, геометрия Евклида рассматривает только структуру из точек, лежащих на поверхности сферы, радиус которой является модулем пространственного комплекса с действительными параметрами. Это заключение остается в силе и для комплексного пространства более высокой размерности, согласно формулам.
При определенных соотношениях аргументов, характеризующих вложенные друг в друга пространства разной по величине размерности, интервал равен корню квадратному из квадратов значений координат. Интервал дается в этом случае только для точек, лежащих на поверхности структурной сферы.
Если использовать не декартовые координаты, а например, сферические, цилиндрические, то квадрат расстояния между соседними точками в этих координатах принял бы вид
, где -метрический тензор евклидова пространства, а суммирование идет по одинаковым индексам .
Появление метрического тензора является следствием задания точки как совмещение в ней значений координат. Точка при этом не определяется одним комплексным параметром. Этот момент был подробно разобран выше.
Б.Риман (B.Rieman), развивая идею Н.И.Лобачевского и К.Ф.Гаусса (K.F.Gauss) ввел переменный метрический тензор , оставив фому записи квадрата интервала прежней. Это означало, что кривизна пространства в римановой геометрии отлична от нуля. Риманова геометрия лежит в основе ОТО А. Эйнштейна. Метрический тензор определяется как функция зависимости кривизны пространства от тензора энергии –импульса.
В РТГ А.Логунов использует геометрию, структура которой определяется интервалом
, где С –скорость света, t-время.
Геометрия, определяемая таким интервалом, называется псевдоевклидовой, а четырехмерное пространство с такой геометрией пространством Минковского (Minkowski).
Интервал в этом виде равен нулю, когда все дифференциалы равны нулю и фактически рассматривается одна точка. Во втором случае интервал принимается равным нулю, когда квадрат временной координаты равен сумме квадратов пространственных координат. Второй вариант в четырехмерном пространстве это грубейшая ошибка теоретической физики. Интервал в четырехмерном пространстве нельзя рассматривать вне зависимости от связи координат через аргументы. Это также неоднократно подчеркивалось в исследованиях.
Световой конус теории относительности имеет совершенно другую структуру, чем его равенство нулю. Световой конус характеризует разложение пространства на два не суммируемых пространства, которые образуют подпространство из мнимых точек.
Интервал при этом имеет одинаковый вид в бесконечном классе систем отсчета, движущихся одна относительно другой с постоянной скоростью, меньшей скорости света. Преобразования от одной инерциальной системы к другой, сохраняющий вид интервала, называются преобразованиями Лоренца (Lorentz). Применение такой геометрии привело к принципиально различным результатам в теориях ОТО А.Эйнштейна и РТГ А.Логунова.
Применение такой геометрии привело к принципиально различным результатам в теориях ОТО А.Эйнштейна и РТГ А.Логунова.
В комплексном пространстве интервал Минковского дает возможность исследовать новые структурные свойства пространства-времени.
Рассмотрим комплекс
Комплекс имеет три действительных и один комплексный параметр . Пространственный интервал выступает как одна координата по отношению к временной координате
.
Запишем комплекс в виде
|
(10.17.1) |
Если скорость V в структуре комплекса достигает скорости света С=V, то комплекс принимает вид
.
Рассмотрим процесс выделения подпространства в комплексе
|
(10. |
Сравнивая формулы (10.17.1) и (10.17.2) приходим к однозначному выводу: подпространство движется в пространстве со скоростью света С относительно ядра комплекса. Подпространство характеризуется сингулярным значением аргумента и мнимыми пространственными точками, так как и характеризует разложение подпространства на два не суммируемых комплекса.
Комплексное пространство в данном случае представляет сумму из пространства-ядра меньшей по величине размерности плюс подпространство из мнимых точек, выступающее по отношению к ядру как заряженная оболочка или полевая оболочка.
Рис. 102. электронное нейтрино .
Лептонный заряд определяется положительным изолированным аргументом , определенным в верхнем и нижнем полупространстве. Отрицательная спиральность нейтрино задается поворотом центрального комплекса (действительного радиуса) на угол , против часовой стрелки. Пространство нейтрино представлено в координатах
Пространство нейтрино представлено в координатах
Ядро нейтрино есть комплекс в смысле Коши . Координаты мнимых точек
Рис. 103. Электронное
антинейтрино
.
Рис. 104. Мюонное нейтрино.
Лептонный заряд определяется отрицательным изолированным аргументом , определенным в верхнем и нижнем полупространстве. Положительная спиральность определяется поворотом ядра комплекса на угол по часовой стрелки. Координаты мнимых точек
.
Мюонное нейтрино имеет в ядре два комплекса. Нейтральный комплекс как результат аннигиляции нейтрино и антинейтрино . Второй комплекс ядро заряженного нейтрино
. В данном случае положительно заряженное нейтрино с положительным лептонным зарядом где
.
Рис.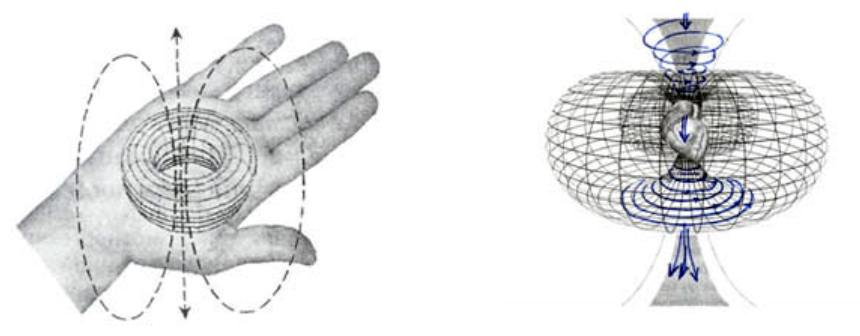 105. Структура заряженных подпространств электрона в комплексных координатах
105. Структура заряженных подпространств электрона в комплексных координатах
Ядро электрона представлено комплексом , где сумма углов относится к верхнему полупространству, разность к нижнему.
Лептонный заряд электрона определен положительным изолированным направлением в лептонном пространстве
Электрический заряд электрона определен отрицательным изолированным направлением в электронном пространстве
Мнимые точки электрического заряда заканчиваются лептонным образованием с положительным зарядом
В результате оболочка электрона заряжена двойным зарядом: электрическим и лептонным
По ориентации мнимых единиц 1
,i,j в пространстве можно судить о поворотах подпространств.
Ядра могут содержать скомпенсированные заряды.
Замена комплексов ядер на мюонное нейтрино или Тау-нейтрино дает мюон или соответственно -лептон. На рис это фиксируется заполнением ядер
.
Рис.106. Структура положительно заряженного пиона
.
Структура представлена в координатах пространства . Пион обладает только электрическим зарядом. Лептонный заряд аннигилирован. В центре ядро нейтрального комплекса.
Электрический заряд отождествляется с изолированным направлением
Структура положительного каона повторяет структуру положительно заряженного пиона (рис. 106.) с добавлением в ядро нейтрального комплекса , который возникает в результате аннигиляции электрического и лептонного пространств, так что
Для ядра каона имеем сумму ядер положительного пиона и ядра нейтрального пиона
.
Рис 107 Пространство протона
.
Протон обладает барионным и электрическим зарядом. Барионное пространство имеет координаты
Координатные оси представляют цилиндрические оси, заполненные нейтринными пространствами, которые совместно образуют электронное пространство . Третья координатная ось заполнена пространством
.
Барионный заряд определяется изолированным направлением
Положительный электрический заряд определяется положительным пионом , входящим в ядро пространства протона и в пространство, образованное двумя координатными осями . Пространство пиона представлено на рис 5 входит в барионное пространство.
В барионное пространство протона может входить заряженный положительно пион , каон
, и т. д.
д.
В тоже время протон может представлять целую периодическую систему из заряженных пионов , и нейтральных
.
[Следующий
параграф]
Мини
оглавление:
[0], [1.1.1, 1.1.2, 1.1.3,
1.1.4, 1.1.5, 1.1.6,
1.1.7, 1.1.8, 1.2,
1.2.1, 1.2.2, 1.2.2.a,
1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1,
1.3.2, 1.3.3, 1.3.4,
1.3.5, 1.3.6, 1.4.1,
1.4.2, 1.5, 1.6, 1.7.1, 1.7.2,
1.7.3.1, 1.7.3.2, 1.7.3.3,
1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3,
3.4.1, 3.4.2, 3.4.3,
3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3,
5.4, 5.4.Т1, 5.4.Т2,
5.4.Т3, 5.5.1, 5.5.2,
5.5.3, 5.5.4],[6.1.1,
6.1.2, 6.2.1, 6.2.2,
6.2.3, 6.2.4, 6.2.5,
6.3, 6.4.1, 6.4.2,
6.5.1, 6.5.2],[7.1,
7.2, 7.3, 7.4,
7.5, 7.6, 7.7.1,
7.7.2, 7.8.1, 7.8.2,
7.8.3, 7. 9],[8.1,
9],[8.1,
8.2.1, 8.2.2, 8.3,
8.4, 8.5, 8.6,
8.6.T1, 8.7, 8.8.1,
8.8.2, 8.8.3, 8.9.1,
8.9.2, 8.9.3, 8.10,
8.10.T2, 8.10.T3],[9.1,
9.2, 9.3, Рис.88,
89, 90, 91,
92, 93, 94,
95, 96, 97,
98, 99, 100],[10.1,
10.2, 10.3, 10.4,
10.5, 10.6, 10.7,
10.8, 10.9, 10.10,
10.11, 10.12, 10.13,
10.14, 10.15.1, 10.15.2,
10.16.1, 10.16.2, 10.17,
10.18],[11]
Размещенный материал является
электронной версией книги: ©
В.И.Елисеев, «Введение в методы теории функций
пространственного комплексного переменного»,
изданной Центром научно-технического
творчества молодежи Алгоритм. — М.:,
НИАТ. — 1990. Шифр Д7-90/83308. в каталоге
Государственной публичной научно-технической
библиотеки.
Сайт действует с 10 августа 1998.
E-mail: [email protected]
Электромагнитная составляющая физического вакуума как основной энергосодержащей среды эфира Вселенной: Феноменология
ПОЛУЧИТЬ ПРИЛОЖЕНИЕ
Электромагнитная составляющая физического вакуума как основной энергосодержащей среды эфира Вселенной: Феноменология
ISSN: 2329-6542
Открытый доступ
Отправить рукопись
arrow_forward
arrow_forward
3 rd Международная конференция по физике высоких энергий
11-12 декабря 2017 г. | Рим, Италия
| Рим, Италия
Тимашев Сергей Ф.
Институт физической химии им. Карпова, Россия
Рефераты научных направлений : J Astrophys Aerospace Technol
Abstract :
Сегодня можно говорить о кризисе современной астрофизики. Величина космологической постоянной ??, которая в соответствии с уравнениями общей теории относительности (ОТО) Эйнштейна определяется плотностью энергии ?µ?½ физического вакуума, превышает экспериментально определяемое значение на 120 порядков, если для расчетов используются общепринятые представления о динамике Большого взрыва. В докладе будет показано, что физическую сущность возникающих проблем следует прежде всего понимать на уровне трансцендентальной феноменологии. Основанием для создания соответствующей феноменологической конструкции является введение в физическую науку базовой энергосодержащей среды, своего рода эфира, который отождествляется с электромагнитной составляющей физического вакуума ?? ЭМ вакуум, который считается базовой системой отсчета, связанной с расширяющейся Вселенной. Считается, что Вселенная является открытой системой и источником энергии, питающей Вселенную, является внешний ложный вакуум, более энергоемкий, чем ЭМ-вакуум нашей Вселенной. Предполагается, что энергетическая сила, которая постоянно питает нашу вселенную через границу ложного вакуума — ?? ЭМ вакуум равен мощности Планка. При этом поступающий во Вселенную поток энергии определяет после учета уравнения Хаббла уравнение динамики расширения Вселенной (аналог первого уравнения Фридмана), а скорость увеличения объема Вселенной определяет рабочее давление. Показано, что рассчитанная на основе таких представлений плотность энергии ?µ?½calc ЭМ вакуума находится в полном соответствии с величиной ?? (решение задачи 120 заказов). В соответствии с общей идеей Казимира все элементарные частицы и атомные ядра во Вселенной открыты для ЭМ вакуума, и в окрестности каждой элементарной частицы или атомного ядра формируется Казимировская поляризация ЭМ вакуума. Показано, что именно в рамках таких представлений можно понять сущность явления гравитации и происхождение уникальной малости гравитационного взаимодействия по сравнению с ядерным (сильным и слабым) и электромагнитным взаимодействием.
Считается, что Вселенная является открытой системой и источником энергии, питающей Вселенную, является внешний ложный вакуум, более энергоемкий, чем ЭМ-вакуум нашей Вселенной. Предполагается, что энергетическая сила, которая постоянно питает нашу вселенную через границу ложного вакуума — ?? ЭМ вакуум равен мощности Планка. При этом поступающий во Вселенную поток энергии определяет после учета уравнения Хаббла уравнение динамики расширения Вселенной (аналог первого уравнения Фридмана), а скорость увеличения объема Вселенной определяет рабочее давление. Показано, что рассчитанная на основе таких представлений плотность энергии ?µ?½calc ЭМ вакуума находится в полном соответствии с величиной ?? (решение задачи 120 заказов). В соответствии с общей идеей Казимира все элементарные частицы и атомные ядра во Вселенной открыты для ЭМ вакуума, и в окрестности каждой элементарной частицы или атомного ядра формируется Казимировская поляризация ЭМ вакуума. Показано, что именно в рамках таких представлений можно понять сущность явления гравитации и происхождение уникальной малости гравитационного взаимодействия по сравнению с ядерным (сильным и слабым) и электромагнитным взаимодействием. Можно предположить, что именно волновое распространение электромагнитного возмущения вакуума было зарегистрировано в недавних наблюдениях LIGO, и это возмущение могло возникнуть при столкновении двух нейтронных звезд или каких-то других крупномасштабных событиях. Последние публикации 1. Тимашев Сергей (2017) О явлении гравитационного экранирования Physical Science International Journal 13(1)1-6. 2. Тимашев Сергей (2017) Метастабильные ненуклонные состояния ядерной материи: Феноменология. Международный журнал физических наук 15 (2): 1-25. 3. Тимашев Сергей (2014) Планковский источник энергии-массы и динамика Вселенной: феноменология. Международный журнал астрофизики и космических наук 2(3)33-45. 4. Тимашев Сергей (2015) Оценка средней плотности энергии электромагнитной составляющей физического вакуума и квантовая природа гравитации. Международный журнал астрофизики и космических наук 3(4)60-64. 5. П. Эбботт и соавт. (2016) Наблюдение гравитационных волн от слияния двойных черных дыр. Письма о физическом обзоре 116: 061102.
Можно предположить, что именно волновое распространение электромагнитного возмущения вакуума было зарегистрировано в недавних наблюдениях LIGO, и это возмущение могло возникнуть при столкновении двух нейтронных звезд или каких-то других крупномасштабных событиях. Последние публикации 1. Тимашев Сергей (2017) О явлении гравитационного экранирования Physical Science International Journal 13(1)1-6. 2. Тимашев Сергей (2017) Метастабильные ненуклонные состояния ядерной материи: Феноменология. Международный журнал физических наук 15 (2): 1-25. 3. Тимашев Сергей (2014) Планковский источник энергии-массы и динамика Вселенной: феноменология. Международный журнал астрофизики и космических наук 2(3)33-45. 4. Тимашев Сергей (2015) Оценка средней плотности энергии электромагнитной составляющей физического вакуума и квантовая природа гравитации. Международный журнал астрофизики и космических наук 3(4)60-64. 5. П. Эбботт и соавт. (2016) Наблюдение гравитационных волн от слияния двойных черных дыр. Письма о физическом обзоре 116: 061102.
Биография :
Сергей Ф. Тимашев — профессор физики Российского университета дружбы народов, Москва. Он также является старшим научным сотрудником USPolyResearch, США. И он заведующий лабораторией мембранных процессов. Карпова Институт физической химии, Москва
PDF
HTML
50+ миллионов читателей
Основные моменты журнала
Отчет о цитировании Google Scholar
Цитаты: 89
Астрофизика и аэрокосмические технологии получили 89 ссылок согласно отчету Google Scholar
Процесс рецензирования астрофизики и аэрокосмических технологий подтвержден в публикациях
Индексировано в
Ссылки по теме
Журналы открытого доступа
arrow_upward
arrow_upward
Вакуумные конденсаты и эксперименты с «эфирным ветром» — arXiv Vanity
Вакуумные конденсаты и эксперименты с эфирным ветром
М. Консоли, А. Пагано и Л. Паппалардо
Консоли, А. Пагано и Л. Паппалардо
Istituto Nazionale di Fisica Nucleare, Sezione di Catania
и Dipartimento di Fisica dell’ Università 60 Sofia
4 Via
9 , 95123 Catania, Italy
Abstract
Идея «конденсированного» состояния вакуума общепринята.
в современной физике элементарных частиц. Мы утверждаем, что
это должно мотивировать новое поколение точных
эксперименты по «эфирному ветру» с современными технологиями.
1. Представление о «конденсированном» вакууме общепринято.
в современной элементарной частице
физика. Действительно, во многих различных контекстах вводится набор
элементарные кванты, пертурбативное «пустое» вакуумное состояние |o⟩ которых не
физическое основание взаимодействующей теории.
В физически релевантном случае Стандартной модели
ситуацию можно резюмировать, сказав [1] , что
«То, что мы переживаем как
пустое пространство есть не что иное, как конфигурация поля Хиггса, имеющая
минимально возможная энергия. Если мы перейдем от полевого жаргона к жаргону частиц, это
Если мы перейдем от полевого жаргона к жаргону частиц, это
означает, что пустое пространство на самом деле заполнено частицами бозона Хиггса. У них есть
Бозе сжался».
В этом случае, когда
конденсирующиеся кванты — это всего лишь нейтральные бесспиновые частицы
(«фионы» [2] ),
перевод с «жаргона поля на жаргон частиц»,
составляет установление четко определенной функциональной связи (см. ссылку [2] )
n=n(ϕ2) между средней плотностью частиц
n в режиме k=0 и среднее значение скаляра
поле ⟨Φ⟩=ϕ.
Таким образом, бозе-конденсация является лишь следствием
условие минимизации
эффективный потенциал Veff(ϕ). Это имеет абсолютный
минимумы при некоторых значениях ϕ=±v≠0, для которых n(v2)=¯n≠0
[2] .
Симметричная фаза, где ⟨Φ⟩=0 и n=0,
в конечном итоге будет восстановлен на этапе
температура перехода T=Tc. Это в Стандартной модели так высоко
что можно безопасно аппроксимировать обычный вакуум как нулевой температуры
системе (для сравнения подумайте о 4He при
температура 10−12 oK).
Это наблюдение служит аргументом в пользу
представить вакуум как квантовую бозе-жидкость, т.е. среду
где тела могут течь без видимого трения, как в сверхтекучем 4Не,
в согласии с результатами эксперимента.
С другой стороны, конденсированный вакуум физики элементарных частиц, хотя и отличается от
от эфира классической физики, также отличается от
«пустое» пространство-время специальной теории относительности, которое предполагается в основе
аксиоматическая квантовая теория поля.
Поэтому, следуя этому ходу мысли,
можно спросить,
макроскопическое заполнение одного и того же кванта
состояние (k=0 в данной системе отсчета)
может представлять собой оперативную конструкцию
«квантового эфира», существование которого
могут быть обнаружены через
точный эксперимент с «эфирным ветром», подобный тому, который проводился в конце
XIX века и в первой половине ХХ века. Этот
вопрос ведет
к основному вопросу лоренц-ковариантного описания вакуума
что будет рассмотрено в следующем разделе.
2. Несмотря на широкое признание, вакуумная конденсация обычно
Несмотря на широкое признание, вакуумная конденсация обычно
считается просто
удобный способ изменить набор исходных степеней свободы.
С этой точки зрения,
все различия между физическим вакуумом и пустым пространством считаются
быть реабсорбируемым в
некоторые основные параметры, такие как массы частиц и несколько физических
констант, оставляя для остальных точную лоренц-ковариантную теорию.
На более формальном основании мы замечаем, однако, что сосуществование
точная ковариация Лоренца и вакуумная конденсация в эффективных
квантовых теорий поля не так тривиальна. Фактически, как следствие
нарушения локальности в энергетическом масштабе, фиксируемом
ультрафиолетовая отсечка Λ [3] ,
можно столкнуться с нелоренц-ковариантом
инфракрасные эффекты, которые зависят от структуры вакуума.
Это явление можно объяснить очень просто, начиная с
наблюдение, что,
в теории отсечки элементарный
кванты рассматриваются как «твердые сферы» радиуса a∼1/Λ,
что касается молекул обычных
иметь значение. Однако по той же причине простая идея
Однако по той же причине простая идея
что отклонения от лоренц-ковариации имеют место только на шкале отсечки
это неверно. На самом деле верно, что в пертурбативном пустом вакуумном состоянии
(без конденсированных квантов) нелокальность ограничена очень коротким
длины волн 2π/|k|≤a.
Однако в
конденсированного вакуума, твердые сферы будут «соприкасаться» друг с другом, создавая
к распространению длинноволнового
флуктуации плотности, которые по определению
не может быть описан лоренц-ковариантным способом.
Для обозначения этого типа инфракрасно-ультрафиолетового соединения, исходящего
из вакуумной конденсации в эффективных квантовых теориях поля,
Воловик [4] ввел очень подходящее название:
повторные нарушения специальной теории относительности в низкоэнергетическом углу.
В простейшем случае спонтанного нарушения симметрии в
λΦ4, где уплотняющая
кванты — это просто нейтральные бесспиновые частицы, эффекты «возвращения» уменьшают
к малой оболочке трехимпульсов, скажем, |k|<δ, где
энергетический спектр отклоняется от лоренц-ковариантной формы. А именно,
А именно,
обозначая MH как типичную энергетическую шкалу, связанную с
Лоренц-ковариантную часть энергетического спектра находим
δMH→0 только при
MHΛ→0.
Основной ингредиент для обнаружения таких «повторно входящих»
эффектов в нарушенной фазе состоит в чисто
квантово-теоретический результат:
связный четырехимпульсный пропагатор G−1(k=0)
является двузначной функцией
[5, 6] . На самом деле, помимо известного решения
G−1a(k=0)=M2H, также находим
G−1b(k=0)=0.
Раствор b-типа
соответствует процессам, при которых поглощается (или излучается)
очень маленький 3-импульс k→0
не требует конечной энергии. Эта ситуация хорошо
известна в конденсированной среде, где малая
3-импульс может быть когерентно распределен
среди большого числа элементарных составляющих и соответствует
гидродинамический режим пульсаций плотности,
длины волн 2π/|k| больше
чем рмфп,
длина свободного пробега элементарных составляющих.
Данная интерпретация [7, 8]
беззазорной ветви, что очень естественно на основе общего
аргументы, неизбежна в сверхтекучей среде. Фактически,
Фактически,
«Любая квантовая жидкость, состоящая из частиц с целым
спин (такой как жидкий изотоп 4He) обязательно должен иметь спектр
такого типа… В квантовой бозе-жидкости элементарные возбуждения с малыми
импульсы k (длины волн большие по сравнению с расстояниями между атомами)
соответствуют обычным гидродинамическим звуковым волнам, т.е. являются фононами. Этот
означает, что энергия таких квазичастиц является линейной функцией их
импульс» [9] . В этом смысле сверхтекучее
вакуум обеспечивает для k→0 универсальную картину.
Этот результат не зависит
о деталях ближнего взаимодействия и даже о характере
из элементарных составляющих.
Например, такое же грубое описание можно найти в
сверхтекучий фермионный вакуум [10] , что по сравнению с бозоном Хиггса
вакууме, несут такое же отношение сверхтекучего 3Не к сверхтекучему 4Не.
Таким образом, есть
два возможных типа возбуждений с одинаковыми квантовыми числами, но
разных энергий при 3-импульсе k→0:
одна частица
массивный, с Ea(k)→MH, и коллективный
без зазора с
Еб(к)→0. «Априори», они оба могут распространяться
«Априори», они оба могут распространяться
(и мешать) в фазе нарушенной симметрии.
Поэтому ситуация очень похожа на
сверхтекучий 4He,
где наблюдаемый энергетический спектр обусловлен
переход от «фононной ветви» к «ротонной ветви» в импульсной шкале
|ко| где
| Эфонон(ко)~Эротон(ко) | (1) |
Аналог конденсата Хиггса составляет
энергетический спектр со следующими ограничивающими свойствами:
i) E(k)→Eb(k)=cs|k|
для к→0
ii) E(k)→Ea(k)=MH+k22MH
для |k|≳δ
где
характерный масштаб импульса δ≪MH, при котором
Ea(δ)∼Eb(δ) отмечает переход от коллективного к
одночастичные возбуждения. Это происходит в течение
| δ∼1/rmfp | (2) |
где [11, 12]
| rmfp∼1¯na2 | (3) |
— длина свободного пробега phion,
при заданном значении плотности фионов n=¯n и a
заданное значение длины фион-фионного рассеяния a.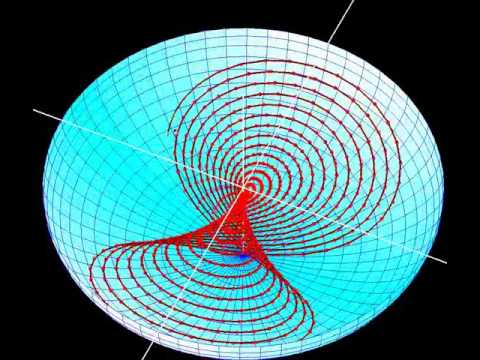 С точки зрения
С точки зрения
тех же количествах, также можно найти [2]
| M2H∼¯на | (4) |
дающие тренд безразмерных отношений (Λ~1/a)
| δMH∼MHΛ∼√¯na3→0 | (5) |
в континуальном пределе, где a→0 и шкала масс ¯na равна
удерживается фиксированным.
Принимая во внимание приведенные выше результаты, физический
разложение скалярного поля по
разорванная фаза может быть удобно
выражается как (phys=’физический’) [13]
| Φфиз(х)=vR+h(х)+Н(х) | (6) |
с
| h(x)=∑|k|<δ1√2VEk[~hkei(k.x−Ekt)+(~hk)†e−i(k.x−Ekt)] | (7) |
и
H(x)=∑|k|>δ1√2VEk[~Hkei(k. x−Ekt)+(~Hk)†e−i(k.x−Ekt)] x−Ekt)+(~Hk)†e−i(k.x−Ekt)] | (8) |
, где V — объем квантования, а
Эк=кс|к| при |k|<δ, а
Ek=√k2+M2H для |k|>δ. Также,
csδ∼MH.
Уравнения (6)-(8) заменить
более традиционные отношения
| Φфиз(х)=vR+H(х) | (9) |
где
| H(x)=∑k1√2VEk[~Hkei(k.x−Ekt)+(~Hk)†e−i(k.x−Ekt)] | (10) |
с Ek=√k2+M2H.
уравнения (9) и (10)
получаются в пределе
δMH∼MHΛ→0
где h(x) исчезает, а нарушенная фаза имеет
только массивные возбуждения, таким образом восстанавливая точно лоренц-ковариантную теорию.
3. Теперь вернемся к основному вопросу, поставленному в конце
Секция 1.
Для конечных значений Λ существуют длинноволновые плотности
колебания вакуума и
Лоренц-ковариация не является точной. Поэтому при наличии таких
эффекты, можем ли мы попытаться
обнаружить наличие скалярного конденсата с помощью точного
Эксперимент «эфирный ветер»?
Сначала заметим, что
простая физическая интерпретация длинноволновой плотности
поле флуктуаций
| φ(x)≡h(x)vR | (11) |
был предложен в
исх. [7, 8] . Представляем GF≡1/v2R
[7, 8] . Представляем GF≡1/v2R
и выбор
масштаб импульса δ как
| δ=√GNM2HGF | (12) |
(GN — постоянная Ньютона) получается идентификация
| φ(x)=UN(x) | (13) |
UN(x) — потенциал Ньютона. Действительно, с выбором в
Уравнение (12) в первом порядке по φ и
в пределах медленных движений уравнения
движение по φ сводится к
уравнение Пуассона для потенциала Ньютона UN [7, 8]
так что отклонения от
Ковариация Лоренца имеет гравитационную силу. Если, как в Стандартной модели,
GF считается константой Ферми, тогда
находит δ∼10−5 эВ и rmfp∼1/δ=O(1) см. Как и предполагалось, вариация
φ(x) имеет место на расстояниях
которые больше, чем rmfp и, следовательно,
бесконечно велико в масштабах элементарных частиц. Также, вводя
MPlanck=1√GN, и используя уравнения (5) и
(12) находим Λ=qHMPlanck с
qH=√GFM2H=O(1), или
a∼1/Λ∼10−33 см.
При этом в первом порядке наблюдаемая
эффекты φ могут быть повторно поглощены [8]
в эффективную метрическую структуру
| ds2=(1+2φ)dt2−(1−2φ)(dx2+dy2+dz2) | (14) |
, что согласуется с первым приближением к линейному элементу
Общая теория относительности [14, 15] .
С этой точки зрения,
искривление пространства-времени возникает из-за изменения масштаба
единиц пространства-времени и от показателя преломления для
распространение света
| Н(ф)~1-2ф | (15) |
чтобы скорость света в кадре конденсата
(в единицах c=2,9979…1010 см/с) составляет
| u∼1+2φ | (16) |
Теперь в общих чертах и
в рамках специальной теории относительности (см. стр. 145 ссылки [16] ),
значение N≠1 подразумевает ненулевое
коэффициент аэродинамического сопротивления k
| к=1−1N2∼−4φ | (17) |
, так что для наблюдателя S′, движущегося относительно
конденсатной системе отсчета со скоростью v и до первого порядка,
свет будет распространяться со скоростью
| u′(v)=u−kv | (18) |
как для стандартных преобразований Галилея с
приведенная относительная скорость kv.
4. Этот тип пространственно-временной картины естественным образом приводит к
классические эксперименты по «эфирному ветру», выполненные
Майкельсон и Морли [17] , Иллингворт [18] и
Миллер [19] , которые были
недавно повторно проанализированы Кэхиллом и Китто [20] .
Их вывод очень прост и предлагает решение
давняя проблема, связанная с
характер наблюдаемых эффектов.
А именно, предусмотренные в тех старых
экспериментах учитывается показатель преломления
Nсредний
диэлектрической среды, используемой в интерферометре
(воздух или гелий), наблюдения
стать последовательным [20] со скоростью Земли
veth=365±18 км/сек
извлеченный из подгонки к данным COBE для
фоновое космическое излучение [21] . На самом деле, краевые сдвиги
пропорциональна
v2earthc2(1−1N2medium), а не
сам v2earthc2.
Кэхилл и Китто использовали в своем выводе «лоренцевский» подход. В этом
точки зрения, на измерительные устройства динамически воздействует их абсолютная
движение таким образом, что это движение становится ненаблюдаемым
[22, 23] . Однако если свет распространяется в среде с
Однако если свет распространяется в среде с
Nmedium≠1, имеется небольшое несоответствие, так что абсолютное
движение может стать наблюдаемым.
В дальнейшем мы будем утверждать, что этот эффект не в
противоречие со специальной теорией относительности.
С этой целью введем наблюдателя S′, который движется в бесконечности,
изотропная и однородная среда, определяющая наблюдателя S.
Давайте также рассмотрим
два световых луча, скажем, 1 и 2, которые перпендикулярны в S
где они распространяются вдоль осей x и y со скоростями
ux(1)=uy(2)=u=cNсреда.
Предположим также, что скорость v вектора S′ направлена вдоль оси x.
В этом случае для оценки скоростей 1 и 2 для
S′, мы можем применить преобразования Лоренца с результатом
| u′x(1)=u−v1−uvc2 u′y(1)=0 | (19) |
и
| u′x(2)=−v u′y(2)=u√1−v2c2 | (20) |
Таким образом, преобразование Лоренца эквивалентно
локальная анизотропия, которая
становится все больше и больше, увеличивая значение v.
Теперь определим L’A и L’B как длины двух
оптические пути, скажем A и B, как
измеряется в кадре S’. Например, они могут представлять
длины
плеч интерферометра, покоящегося в S’-системе.
В первой экспериментальной установке рука
длины L′A берется вдоль направления движения, связанного с балкой
1, а плечо длиной L’B лежит вдоль направления луча 2.
Обратите внимание, что два плеча в кадре S ‘образуют угол
чем отличается от 90o в терминах O(v/c).
Таким образом, используя приведенные выше результаты,
время прохождения луча 1 вперед и назад по L’A равно
| T’A=L’A(1-uv/c2u-v+1+uv/c2u+v)~2L’Au(1+kmediumv2u2) | (21) |
где
| кмсреда=1−1N2среда | (22) |
Чтобы оценить время T′B,
чтобы балка 2 шла вперед и назад по плечу длиной
L′B, нужно сначала вычислить
модуль его скорости в S′ системе отсчета
| u′=√(u′x(2))2+((u′y(2))2=u√1+kmediumv2u2 | (23) |
, а затем использовать соотношение u′T′B=2L′B, получив таким образом
| T′B=2L′Bu′∼2L′Bu(1−kmediumv22u2) | (24) |
Таким образом интерференционная картина между световым лучом, выходящим
оптического пути А и выходящего из оптического пути В,
определяется временем задержки
| ΔT’=T’A-T’B~2L’Au(1+kmediumv2u2)-2L’Bu(1-kmediumv22u2) | (25) |
С другой стороны, если бы луч 2 распространялся по оптическому пути
А и
луча 1 вдоль B, можно было бы получить другую
время задержки, а именно
| (ΔT’)rot=(T’A-T’B)rot~2L’Au(1-kmediumv22u2)-2L’Bu(1+kmediumv2u2) | (26) |
таким образом, чтобы при вращении аппарата
будет сдвиг полосы, пропорциональный
| (ΔT′)−(ΔT′)rot∼3(L′A+L′B)ukmediumv2u2 | (27) |
Таким образом, S’ теперь сможет определить свою «абсолютную»
скорость в полном согласии со специальной теорией относительности. В самом деле, для S′
В самом деле, для S′
Уравнение (27) — единственный способ обнаружить существование
S наблюдатель через
значение скорости v, рабочее определение которой в противном случае
было бы неясно (имея дело с равномерным движением
в бесконечной, изотропной и однородной среде).
С другой стороны, если числовое значение
Nmedium≠1 были неизвестны, S’ попытается определить S
через эффективную, уменьшенную скорость
vobs∼√kmediumv, а не через сам v.
Теперь естественно возникает следующий вопрос. Что произойдет, если мы
удалить среду везде, кроме небольшой области пространства
что включает в себя плечи интерферометра?
Будут ли полосы смещаться при вращении прибора? На первый взгляд,
ответ положительный. На самом деле возникновение смещения полос при вращении
аппарат, находящийся в состоянии покоя в системе S ′
не может зависеть от наличия среды во внешнем
области космоса. Однако после некоторого размышления ответ может
стать отрицательным. Действительно, можно утверждать, что
теперь среда находится в состоянии покоя
кадра S’, так что два световых луча должны распространяться с
с одинаковой скоростью независимо от их ориентации.
Последнее ожидание основано на рассмотрении сейчас
наблюдатель S′ должен быть физически эквивалентен
введенный ранее наблюдатель S (для которого мы предполагали
точно изотропное значение
u=cNсреда везде). Однако,
эта эквивалентность не имеет строгого основания, поскольку, в отличие от
S′ наблюдатель S был взят покоящимся в бесконечной среде.
Таким образом, возникновение (или отсутствие) смещения интерференционных полос становится чисто
экспериментальный выпуск [24] :
способ проверить локальную изотропию.
На практике для скорости Земли и для
O(v2earthc2), можно повторно проанализировать
[20]
эксперименты по эффективному параметру
| ϵ=v2earthu2kmedium≡v2obsc2 | (28) |
и используйте соответствующие экспериментальные значения
Наир ~ 1,00029 или
Нелий ~ 1,000036.
Например, для
vearth=365±18 км/сек (и работающая в воздухе оптическая система)
один предсказывает
ϵ∼10−9 или
vobs∼9 км/сек, точно
Результат Миллера.
Сравнение с экспериментом Кеннеди и
Торндайк тоже можно сделать по тому же принципу.
ограничив свой анализ
длительные наблюдения, где они нашли
ненулевое значение vobs=15±4 км/сек [25] .
Обратите внимание, что тот же анализ может применяться даже к
эксперимент Jaseja et al.
[26] где измеряли
сдвиг Δν по мазерной частоте νc
вводится вращением аппарата так, чтобы
Δννc∼ϵ.
Действительно, результаты показали четко определенный сдвиг
Δν∼275 кГц или примерно на одну часть больше 109 в базовом
частота νc∼3⋅1014 Гц. Однако,
этот экспериментальный эффект, хорошо согласующийся с результатами Миллера [27] ,
не воспринимался всерьез и считался ложным
..предположительно из-за магнитострикции в проставках из инвара из-за
магнитное поле Земли». Для проверки согласованности этого
интерпретация, авторы исх. [26]
действительно планировали повторить свой анализ, заменив потенциально
проблемные части их аппарата. Однако этот усовершенствованный эксперимент
никогда не выполнялся [28] .
5. Теперь мы готовы вернуться к
флуктуации плотности скалярного конденсата рассмотрены в разд.3.
С этой целью наблюдаем
что, согласно Кэхиллу и Китто [20] (и согласно нашему
предыдущий анализ) в
вакуумные эксперименты Joos [29] и
Бриле и зал [30] без эффекта
можно было наблюдать. На самом деле, в этом случае
Nvacuum=1 ровно так, чтобы vobs=0.
Однако даже очень точные Бриле и Холл
можно считать экспериментом
как показывая ненулевой результат, хотя и на уровне
точность ∼10−15 (см. их рис. 3 и соответствующие
подписи к рисунку). Таким образом, можно
размышлять о возможном влиянии ненулевого показателя преломления
Уравнение (15), для которого «в вакууме» все же должно быть
поправки, пропорциональные
| v2earthc2(1−1N2(φ)) | (29) |
Теперь перейдем к обычным единицам и для центрально-симметричного
поле, у одного есть
| φ(R)=-GNMc2R | (30) |
Следовательно, для аппарата, размещенного на поверхности земли, находим
φ(R)∼−0,7⋅10−9 (для M=Mearth и
R=Земля) и
| v2earthc2(1−1N2(φ))∼4⋅10−15 | (31) |
для того же значения vearth=365±18 км/сек извлечено
по данным КОБЕ. Этот крошечный эффект, который
Этот крошечный эффект, который
согласуется с результатами, полученными
Бриле и Холла, можно было бы обнаружить более точным
экспериментировать с современными технологиями и
уровень точности ∼10−16.
Резюмируя: согласно современным представлениям, вакуум не «пуст».
Таким образом, следует тщательно проверять совместимость между
точный Лоренц
ковариация и вакуумная конденсация в эффективных
квантовые теории поля. Для частного случая скалярного конденсата
нелокальность
связанный с наличием ультрафиолетовой отсечки, также будет
проявляются на длинных волнах в виде нелоренц-ковариантных
колебания плотности
связанная со скалярной функцией φ(x).
Если на основании исх. [7, 8] , эти длинноволновые
эффекты естественно интерпретируются в терминах ньютоновского потенциала ООН
(при отождествлении φ=UN) получается
кривизна пространства-времени слабого поля общей теории относительности
показатель преломления N∼1−2φ. Это значение
N(φ) может быть важно для понимания очень
точный (вакуумный) эксперимент по «эфирному ветру» с использованием современных технологий
и уровень точности ∼10−16.
Благодарности
Мы благодарим Д. Маккарроне и Ф. Селлери за полезные обсуждения.
- [1]
Г. ’т Хоофт, В поисках лучших строительных блоков, Кембридж
Университетское издательство, 1997, с. 70. - [2]
М. Консоли и П. М. Стивенсон, Int. Дж. Мод. физ. А15 (2000) 133.
- [3]
H. Salehi и H. R. Sepangi, Phys. лат. А251 (1999) 95.
- [4]
Воловик Г.Е. // Письма в ЖЭТФ. 73 (2001) 162.
- [5]
М. Consoli, Phys. лат. В 512 (2001) 335.
- [6]
М. Consoli, Phys. Версия D65 (2002 г.) 105017. - [7]
М. Consoli, Phys. лат. В541 (2002) 307.
- [8]
М. Консоли, Приближенная лоренц-инвариантность вакуума: физ.
решение «проблемы иерархии»?, arXiv:hep-ph/0306070, отправлено
к физ. Преподобный Д. - [9]
Лифшиц Е.М., Питаевский Л.П. Статистическая физика. Ч. 2.
Pergamon Press Ltd 1980, стр.85. - [10]
GE Volovik, Phys. Отчет 351 (2001) 195.
- [11]
Физическая кинетика.
Pergamon Press Ltd 1981, с. 11.
11. - [12]
П. М. Стивенсон, Существуют ли волны давления в вакууме? , вклад
на конференцию «Нарушения СРТ и лоренц-инвариантности», Университет
Индианы, август 2001 г. World Scientific, arXiv:hep-ph/0109.204. - [13]
Под «физическим» мы подразумеваем, что нормировка вакуумного поля
vR таков, что
квадратичная форма Veff(ϕR) при ϕR=vR в точности
дается физической массой бозона Хиггса M2H. - [14]
Н. Розен, Phys. 15 (1940) 154.
- [15]
С. Вайнберг, Гравитация и космология, John Wiley and Sons, Inc., 1972,
стр. 181. - [16]
Дж. Л. Синг, Относительность: специальная теория, Северная Голландия,
Амстердам 1964. - [17]
А. А. Майкельсон и Э. В. Морли, Phil. Маг. 24 (1887) 449.
- [18]
К. К. Иллингворт, Phys. 30 (1927) 692.
- [19]
DC Miller, Rev. Mod. физ. 5 (1933) 203.
- [20]
Р. Т. Кэхилл и К. Китто, arXiV: Physics/0205070.
- [21]
G.F.Smoot et al., ApJL. 371 (1991) 1. - [22]
Дж.


 И. Числовое поле. Введение в ТФКПП.
И. Числовое поле. Введение в ТФКПП. 17.2)
17.2) 11.
11.